牛顿迭代求解方程
牛顿迭代法的基本思想是，任意给定一个$x_0$，基于下式进行迭代，直到两次计算的差值小于一定的区间，误差在一定的范围内就可以停止计算。在求解高阶方程，或是超越方程时都可以应用此方法。
$ x_{n+1} = x_{n} - \frac{f(x_n)}{f’(x_n)} $
其中$x_n$代表第n次计算后的值。停止的条件可以设置为$ |x_{n+1} - x_{n}| < \varepsilon $.
求解一元三次方程
例如下的方程进行求解：
$10x^3-3x^2-8x-2=0$
首先令$f(x)=10x^3-3x^2-8x-2=0$，显然可以利用导数的知识可以得到函数的单调性（但对于更高阶数的一般方程而言可能会存在一些困难）。利用计算机来绘制图像。
初始点的选取
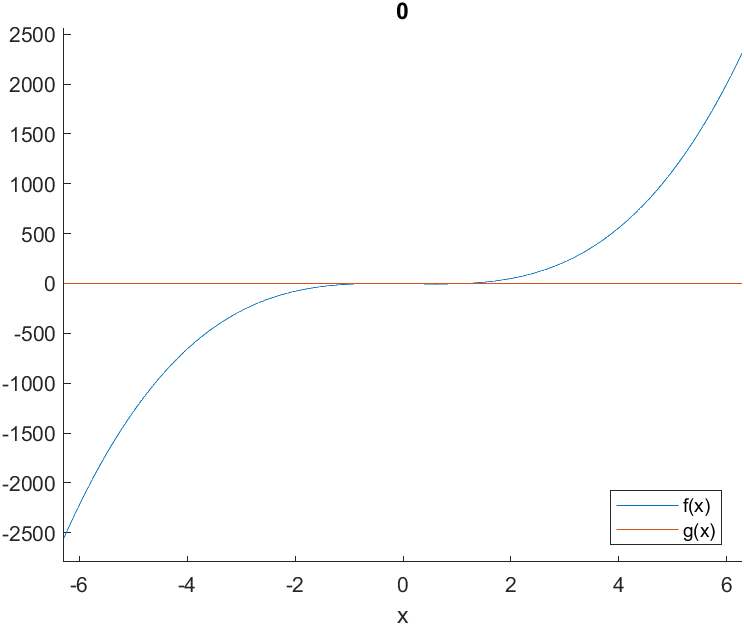
这里，以MATLAB软件为例，使用ezplot函数直接绘制函数图像。同时绘制x轴，辅助参考。
1
2
3
4
5
6
7
syms x;
f=10*x^3-3*x^2-8*x-2;
g=x-x;
hold on
ezplot(f);
ezplot(g);
legend("f(x)",'g(x)')
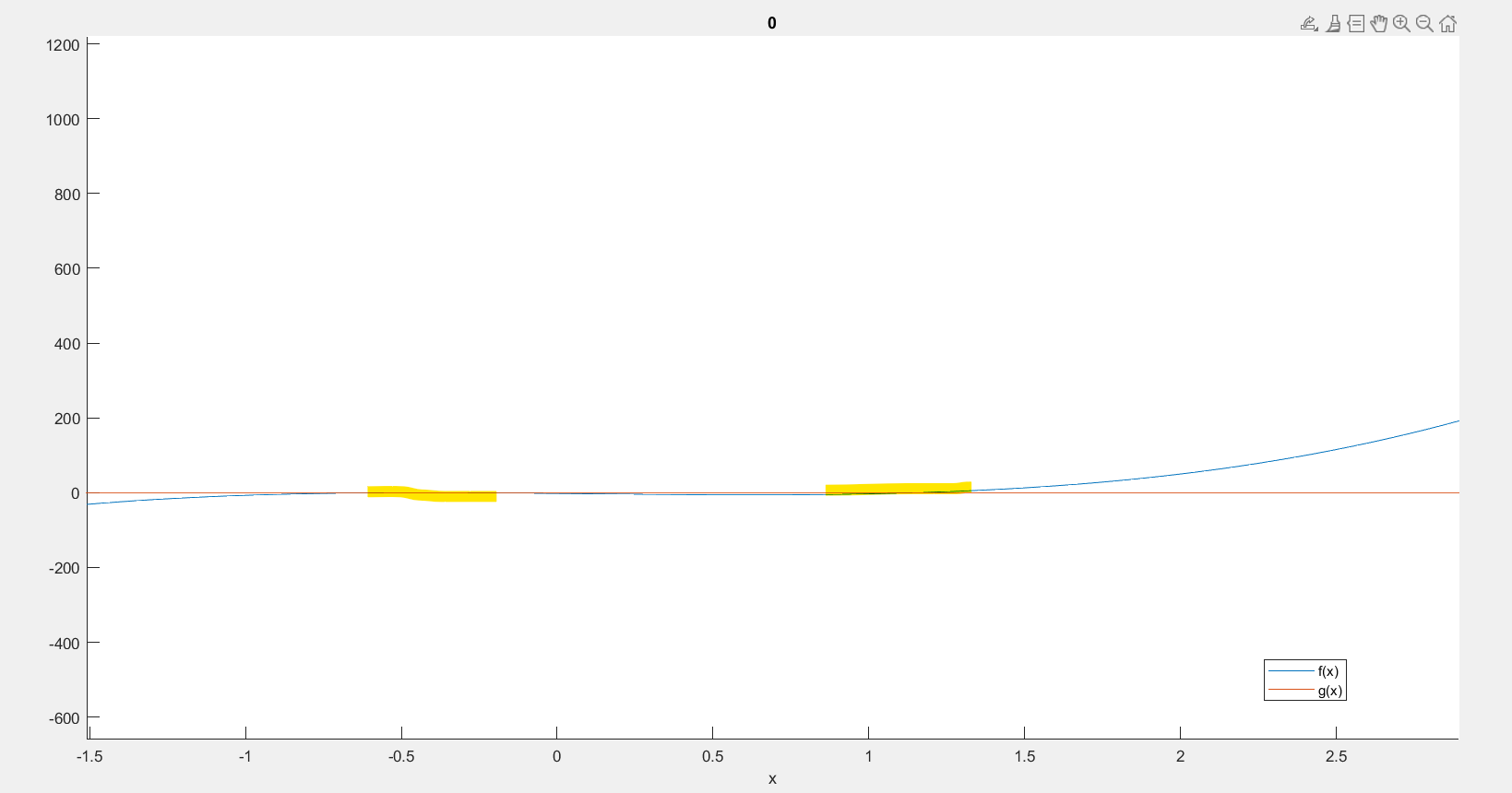观察得到在$y=0$处存在着可疑零点。于是，逐步放大。确实，你可以通过逐步放大寻找方程的根，如果假设是在手画图的情况下，就很难做到这么精准了。尽管如此，我们仍然锁定了在（-2,2）这个区间内，可能存在2个根的嫌疑。（三次方程应当有三个跟）。
对于实际应用题目而言，可以进一步的取舍——这个方程来源于金融学，$x=1+i$，i表示利率。根据我们的常识，我们希望得到的x应该在1~2区间内，而更倾向于在1.1附近。因此，选定牛顿迭代的初始点就在1.1处。所以我们有$x_0=1.1$。（只需大致接近，无需非常精准，避免出现收敛到其他值的情况即可）。
牛顿迭代过程
首先，$x_0=1.1$，我们可以计算出这一点的函数值和导数：
$f(x_0)=10x_0^3-3x_0^2-8x_0-2=-1.12$
$f’(x_0)=30x_0^2-6x_0-8=21.7$
因此$ x_{1} = x_{0} - \frac{f(x_0)}{f’(x_0)} = 1.1-\frac{-1.12}{21.7}=1.1516 $
$f(x_1)=10x_0^3-3x_0^2-8x_0-2=0.0810$
$f’(x_1)=30x_0^2-6x_0-8=24.8759$
因此$ x_{2} = x_{1} - \frac{f(x_1)}{f’(x_1)} = 1.1516-\frac{0.0810}{24.8759}=1.1483 $
$f(x_2)=10x_0^3-3x_0^2-8x_0-2=-0.0007$
$f’(x_2)=30x_0^2-6x_0-8=24.6680$
因此$ x_{3} = x_{2} - \frac{f(x_2)}{f’(x_2)} = 1.1483-\frac{0.0007}{24.6679}=1.1483 $
发现经过三次迭代之后，$ x_{3} $和$ x_{2} $之间相差小于0.0001，因此可以在误差0.0001以内，认为1.1483是一个较为精确的数值解。
